yes ben la perso ça me parle plus car wé, des maths "purs" et c'est tres interessant merci
La 432 Hz
Quand on parle 432 Hz, il faut faire la nuance entre la gamme chromatique tempérée et la gamme pythagoricienne.
La gamme chromatique tempérée : est le système de division de l'octave dans lequel celle-ci est découpée en douze intervalles chromatiques égaux.
http://fr.wikipedia.org/wiki/Gamme_temp%C3%A9r%C3%A9e
Alors si je représente les notes d'un accord (Do Majeur par exemple) sur les 12 positions d'une horloge, je peux transposer la forme géométrique (d'un demi ton ou +, vers la gauche ou la droite) et garder exactement la même distance entre chaque note. Impossible de faire la même chose avec la gamme pythagoricienne car l'espace entre les demi tons n'est pas toujours de 100 cents.
gamme pythagoricienne :
En utilisant le monocorde, on construit un intervalle de quinte pure à partir d'une note de base en prenant les deux tiers de la corde. À partir de cette nouvelle note on prend à nouveau les deux tiers de la corde, ce qui donne une deuxième quinte. En continuant ainsi, on retombe à la 12e quinte sur une note très proche de celle de départ (si on tient compte du principe d'équivalence des octaves).
http://fr.wikipedia.org/wiki/Gamme_pythagoricienne
Pa de doute! L'oreille nous indique ce rapport de quinte parfais ! Et on remarque que c'est pas si dur à construire quand on découvre comment Pythagore a procéder.
Si j'utilise un analyseur de spectre pour visionner les harmoniques d'une forme d'onde (une dent de scie en l'occurance) san filtre, effet, ni rien, encore la, grosse constatation entre les 2 gammes. À partir de la fondamental, calculons le rapport d'harmonique représenté par la quinte (3/2).
LA/A
432 x 1.5 = 648 .... soit pil poil sur le MI suivant.
440 x 1.5 = 660 ... mais le MI est à 659.255 Hz....
DO/C
256 x 1.5 = 384 ... un joli SOL !
261.626 x 1.5 = 392,439 ... ici le SOL est à 391.995
C'est à partir de ce test bien précis que tout a changer pour moi. Si j'ai besoin de "détuner" mes oscilateurs, je vais le faire moi même...
la gamme de pythagore en Hertz

calculé par moi car j'étais tanné de voir de petites différences sur d'autres versions en ligne
certain l'appel le tableau de Plutarque et Nicomaque de Gérase

on voit bien 2 progressions. 2,4,8,16,32,64 .... et 3,9,27,81 ....
désolé je n'ai plus la source de cette image. Si quelqu'un l'a, je serai heureux de rajouter le lien.
Musicalement, la gamme pythagoricienne n'est pas parfaite. On doit composer avec la quinte du loup. Mais y a beaucoups de façon de la contourner au besoin.
Pour moi :
gamme chromatique tempérée = géométrie
gamme pythagoricienne = nombre
Mise à part, un petit test de résonance à faire en gamme de pythagore :
Jouer un RE majeur avec un délais sync (ou n'importe quel accord Majeur/Mineur) Après changer le tempo en tenant votre accord. Et une fois sur une des valeur de BPM bien précise BOUM, on monte au ciel jusqu'à saturer...mais on est dans le monde digital dans ce test) ! Résonance Impossible à reproduire sur la gamme chromatique tempérée. Si on comprend ce qu'est un délais ... je pense qu'il est facile de faire le lien entre la géométrie de certains lieux, leurs emplacements sur des points fort en énergie électromagnétique, via .... la musique.

Sur ses cuisses deux progressions géométriques: une série
1,2,4,8 sur la cuisse gauche et la deuxième
1,3,9,27 sur la cuisse droite
Les Grecs ont nommé les deux séries Lambda et Platon, dans Timaeus les utilise pour décrire l'Esprit du Monde.
Et c'est probablement pourquoi les anciens égyptiens construisirent deux pyramides à Gizéh, la première basée sur 1, Φ, Φ, l'unique triangle dont les côtés sont en progression géométrique, et la deuxième pyramide a les côtés en progression arithmétique de 3, 4, 5.
source : Pacioli - Géométrie sacrée
On s'éloigne de la musique :
Elf Magnetic Model of Matter and Mind, the Origin of Life and the Art of Healing, Theory, Experiments and Proofs
8 Hz et la santé. Expériences sur d'autres fréquences. Correspondances avec la gamme de pythagore et la gamme chromatique tempérée, et +.
http://www.puharich.nl/Bio/Elf_Magnetic_model_of_matter_and_mind.pdf
Le triangle 3,4,5 de pythagore m'a permis de comprendre ce qu'est le temps sidéral et l'espace temps...
Après on peut relier les compas et les équerres à certains mouvements ... pour moi c'est des math et de la géométrie.
Puis l'humanité à passé le dernier degré (359.xxxx) sur un cycle de 360, je pense qu'il n'y a pu grand chose à cacher.
Pour ma part, tout ceci m'a mené vers un cheminement personnel dans lequel je fais mes propres expériences et réflexions.
The Cosmic 432
https://www.youtube.com/watch?v=kUuyeor8f6Q.
(un autre victime de conspiration) Ce n'est pas le1er qui découvre (redécouvre... et reredécouvre) tout ça mais c'est assez bien vulgarisé comme intro au sujet.
http://abouhey1.free.fr/384.htm
J'ai vraiment composer ceci sans préparation, et ici il est très tard. J'espère que c'est lisible et compréensible. Mais je suis tanné de lire et relire la même histoire de Hitler et 432 Hz partout. Pour moi, la mémoire de l'eau (sa structure), 8hz et la santé, les portes / vortex, la lévitation par résonance, Pi et PHI, les math fractales ... tous ces sujets sont bel et bien reliés. Mais faut arrêter de s'épuiser et de se saturer avec des lectures de conspirations et des pages de débats sans arguments solides. Étudions les nombres et la géométrie.
La gamme chromatique tempérée : est le système de division de l'octave dans lequel celle-ci est découpée en douze intervalles chromatiques égaux.
http://fr.wikipedia.org/wiki/Gamme_temp%C3%A9r%C3%A9e
Alors si je représente les notes d'un accord (Do Majeur par exemple) sur les 12 positions d'une horloge, je peux transposer la forme géométrique (d'un demi ton ou +, vers la gauche ou la droite) et garder exactement la même distance entre chaque note. Impossible de faire la même chose avec la gamme pythagoricienne car l'espace entre les demi tons n'est pas toujours de 100 cents.
gamme pythagoricienne :
En utilisant le monocorde, on construit un intervalle de quinte pure à partir d'une note de base en prenant les deux tiers de la corde. À partir de cette nouvelle note on prend à nouveau les deux tiers de la corde, ce qui donne une deuxième quinte. En continuant ainsi, on retombe à la 12e quinte sur une note très proche de celle de départ (si on tient compte du principe d'équivalence des octaves).
http://fr.wikipedia.org/wiki/Gamme_pythagoricienne
Pa de doute! L'oreille nous indique ce rapport de quinte parfais ! Et on remarque que c'est pas si dur à construire quand on découvre comment Pythagore a procéder.
Si j'utilise un analyseur de spectre pour visionner les harmoniques d'une forme d'onde (une dent de scie en l'occurance) san filtre, effet, ni rien, encore la, grosse constatation entre les 2 gammes. À partir de la fondamental, calculons le rapport d'harmonique représenté par la quinte (3/2).
LA/A
432 x 1.5 = 648 .... soit pil poil sur le MI suivant.
440 x 1.5 = 660 ... mais le MI est à 659.255 Hz....
DO/C
256 x 1.5 = 384 ... un joli SOL !
261.626 x 1.5 = 392,439 ... ici le SOL est à 391.995
C'est à partir de ce test bien précis que tout a changer pour moi. Si j'ai besoin de "détuner" mes oscilateurs, je vais le faire moi même...
la gamme de pythagore en Hertz

calculé par moi car j'étais tanné de voir de petites différences sur d'autres versions en ligne
certain l'appel le tableau de Plutarque et Nicomaque de Gérase

on voit bien 2 progressions. 2,4,8,16,32,64 .... et 3,9,27,81 ....
désolé je n'ai plus la source de cette image. Si quelqu'un l'a, je serai heureux de rajouter le lien.
Musicalement, la gamme pythagoricienne n'est pas parfaite. On doit composer avec la quinte du loup. Mais y a beaucoups de façon de la contourner au besoin.
Pour moi :
gamme chromatique tempérée = géométrie
gamme pythagoricienne = nombre
Mise à part, un petit test de résonance à faire en gamme de pythagore :
Jouer un RE majeur avec un délais sync (ou n'importe quel accord Majeur/Mineur) Après changer le tempo en tenant votre accord. Et une fois sur une des valeur de BPM bien précise BOUM, on monte au ciel jusqu'à saturer...mais on est dans le monde digital dans ce test) ! Résonance Impossible à reproduire sur la gamme chromatique tempérée. Si on comprend ce qu'est un délais ... je pense qu'il est facile de faire le lien entre la géométrie de certains lieux, leurs emplacements sur des points fort en énergie électromagnétique, via .... la musique.


Sur ses cuisses deux progressions géométriques: une série
1,2,4,8 sur la cuisse gauche et la deuxième
1,3,9,27 sur la cuisse droite
Les Grecs ont nommé les deux séries Lambda et Platon, dans Timaeus les utilise pour décrire l'Esprit du Monde.
Et c'est probablement pourquoi les anciens égyptiens construisirent deux pyramides à Gizéh, la première basée sur 1, Φ, Φ, l'unique triangle dont les côtés sont en progression géométrique, et la deuxième pyramide a les côtés en progression arithmétique de 3, 4, 5.
source : Pacioli - Géométrie sacrée
On s'éloigne de la musique :
Elf Magnetic Model of Matter and Mind, the Origin of Life and the Art of Healing, Theory, Experiments and Proofs
8 Hz et la santé. Expériences sur d'autres fréquences. Correspondances avec la gamme de pythagore et la gamme chromatique tempérée, et +.
http://www.puharich.nl/Bio/Elf_Magnetic_model_of_matter_and_mind.pdf
Le triangle 3,4,5 de pythagore m'a permis de comprendre ce qu'est le temps sidéral et l'espace temps...
Après on peut relier les compas et les équerres à certains mouvements ... pour moi c'est des math et de la géométrie.
Puis l'humanité à passé le dernier degré (359.xxxx) sur un cycle de 360, je pense qu'il n'y a pu grand chose à cacher.
Pour ma part, tout ceci m'a mené vers un cheminement personnel dans lequel je fais mes propres expériences et réflexions.
The Cosmic 432
https://www.youtube.com/watch?v=kUuyeor8f6Q.
(un autre victime de conspiration) Ce n'est pas le1er qui découvre (redécouvre... et reredécouvre) tout ça mais c'est assez bien vulgarisé comme intro au sujet.
http://abouhey1.free.fr/384.htm
J'ai vraiment composer ceci sans préparation, et ici il est très tard. J'espère que c'est lisible et compréensible. Mais je suis tanné de lire et relire la même histoire de Hitler et 432 Hz partout. Pour moi, la mémoire de l'eau (sa structure), 8hz et la santé, les portes / vortex, la lévitation par résonance, Pi et PHI, les math fractales ... tous ces sujets sont bel et bien reliés. Mais faut arrêter de s'épuiser et de se saturer avec des lectures de conspirations et des pages de débats sans arguments solides. Étudions les nombres et la géométrie.
[citation]edit : "Ré : 288 Hz : La précession de notre planète Terre, Battement idéal du cœur humain au repos" : j'espère que ton coeur ne bats pas a 288 Hz au repos ! cela fait un pouls de 17280 ! [/citation]
xoc, 288, 2 octaves + bas c'est 72. Il doit manquer une partie du texte ou ce n'est pas bien précisé. Tout fonctionne sur un échelle de spectre, de divisions des Hertz.

Pour le liens sur les plantes. Pour ma part ca fonctionne. Ainsi que de placer une pyramide au dessus de la culture. Yannick Van Doorne, Pier Rubesa, Jacques Collins et j'en passe sont de bonnes référence à ce sujet de nos jours.
Je pense aussi que (ca n'engage que moi)
gamme de pythagore = Unité
gamme chromatique tempérée = dispersion
Je tiens à rajouter que je ne pense pas qu'une gamme est "meilleure" que l'autre musicalement. A chacun son choix.
xoc, 288, 2 octaves + bas c'est 72. Il doit manquer une partie du texte ou ce n'est pas bien précisé. Tout fonctionne sur un échelle de spectre, de divisions des Hertz.

Pour le liens sur les plantes. Pour ma part ca fonctionne. Ainsi que de placer une pyramide au dessus de la culture. Yannick Van Doorne, Pier Rubesa, Jacques Collins et j'en passe sont de bonnes référence à ce sujet de nos jours.
Je pense aussi que (ca n'engage que moi)
gamme de pythagore = Unité
gamme chromatique tempérée = dispersion
Je tiens à rajouter que je ne pense pas qu'une gamme est "meilleure" que l'autre musicalement. A chacun son choix.
La gamme de pythagore implique des octaves faux, à moins d'accepter une quinte détunée pour refermer correctement le cycle des quintes : la fameuse quinte du loup.
La gamme tempérée répartit cette erreur sur toutes les quintes, afin qu'il soit moins problématique.
Question de goûts du coup.
Ceci dit on peut s'en affranchir avec les technologies "hermode tuning" et autres trucs du genre, qui repitch dynamiquement les notes d'un accord afin de tomber sur les intervales justes. Ainsi, selon l'accord joué, un do n'aura pas forcément exactement la même valeur, mais il sonnera juste à chaque fois.
La gamme tempérée répartit cette erreur sur toutes les quintes, afin qu'il soit moins problématique.
Question de goûts du coup.
Ceci dit on peut s'en affranchir avec les technologies "hermode tuning" et autres trucs du genre, qui repitch dynamiquement les notes d'un accord afin de tomber sur les intervales justes. Ainsi, selon l'accord joué, un do n'aura pas forcément exactement la même valeur, mais il sonnera juste à chaque fois.
mais oui la quinte du loup, cest bien ce que je disais + haut 
As-tu déjà comparé le même accord en gamme de pythagore et chromatique tempérée xoc ? Pour ma part, celui de la gamme chromatique tempéré me semble telement mou et instable après avoir joué en pythagoricien.
Aussi les disto, saturation, etc .. réagissent tellement différements d'une gamme à l'autre. 2 mondes !

As-tu déjà comparé le même accord en gamme de pythagore et chromatique tempérée xoc ? Pour ma part, celui de la gamme chromatique tempéré me semble telement mou et instable après avoir joué en pythagoricien.
Aussi les disto, saturation, etc .. réagissent tellement différements d'une gamme à l'autre. 2 mondes !
on peut discuter des gammes qui s'en rapprochent, de la différence entre une quinte pure et une quinte juste ... mais ici je veux juste mettre en évidence le choix du LA en 432 Hz, avec la gamme de pythagore et le tableau de Plutarque et Nicomaque de Gérase posté + haut.
En fait tout dépend du contexte.
Par exemple, à quoi bon chercher une quinte juste, quand derrière elle est jouée par des oscillateurs detunés entre eux pour justement créer ce fameux battement qui donne du mouvement ?
Personnellement, cherchant très souvent la dissonance dans des accords, ce n'est pas une question que je me pose souvent.
Mais quand je veux poser un accord juste (ou non, suivant ce que je recherche), j'utilise les différents modes de tuning du virus : tempered, natural ou pure. Il m'arrive de trouver un accord en "pure" beaucoup trop stable et statique, voir ennuyeux.
Tu as raison sur les questions de distorsion, un accord mal tuné réagit très mal à beaucoup de saturation contrairement à un accord juste. Ce n'est d'ailleurs pas pour rien que les "power chords" ont tant de succès chez les guitaristes hard rock et autres styles du genre : ils se comportent très bien face à d'énormes doses de disto.
Le La 432 (ou 444, ou 415, ou autres), j'ai déjà donné mon avis dessus.
edit : quand aux affirmations que 432 Hz est une fréquence résonance de l'eau, je n'ai pas trouvé d'article sérieux qui parlait de cela. On trouve dans certaines publications scientifiques la mention du fait qu'une fréquence de 42 kHz peut casser une molécule d'eau, via un phénomène de résonance. On trouve aussi mention du fait que suivant la teneur en minéraux, la pression, la température, et quelques autres choses, ces fréquences de résonances moléculaires varient.
Qu'est-ce qu'on fait du coup : on réaccorde notre La si écoute de la musique en altitude ?
Par exemple, à quoi bon chercher une quinte juste, quand derrière elle est jouée par des oscillateurs detunés entre eux pour justement créer ce fameux battement qui donne du mouvement ?
Personnellement, cherchant très souvent la dissonance dans des accords, ce n'est pas une question que je me pose souvent.
Mais quand je veux poser un accord juste (ou non, suivant ce que je recherche), j'utilise les différents modes de tuning du virus : tempered, natural ou pure. Il m'arrive de trouver un accord en "pure" beaucoup trop stable et statique, voir ennuyeux.
Tu as raison sur les questions de distorsion, un accord mal tuné réagit très mal à beaucoup de saturation contrairement à un accord juste. Ce n'est d'ailleurs pas pour rien que les "power chords" ont tant de succès chez les guitaristes hard rock et autres styles du genre : ils se comportent très bien face à d'énormes doses de disto.
Le La 432 (ou 444, ou 415, ou autres), j'ai déjà donné mon avis dessus.
edit : quand aux affirmations que 432 Hz est une fréquence résonance de l'eau, je n'ai pas trouvé d'article sérieux qui parlait de cela. On trouve dans certaines publications scientifiques la mention du fait qu'une fréquence de 42 kHz peut casser une molécule d'eau, via un phénomène de résonance. On trouve aussi mention du fait que suivant la teneur en minéraux, la pression, la température, et quelques autres choses, ces fréquences de résonances moléculaires varient.
Qu'est-ce qu'on fait du coup : on réaccorde notre La si écoute de la musique en altitude ?
[citation]... à quoi bon chercher une quinte juste, quand derrière elle est jouée par des oscillateurs detunés entre eux pour justement créer ce fameux battement qui donne du mouvement ?[/citation]
ce n'est pas nécessairement tous les instruments qui seront "détuné". Exemple l'accord plaqué du gros pad l'est, mais pas le lead principal.
[citation]j'utilise les différents modes de tuning du virus : tempered, natural ou pure. [/citation]
je pensais qu'il fallait tout changer l'OS à chaque fois pour faire ce genre de manip avec le virus ?? Tu peux me dire si les valeurs (Hz) du filtre et EQ sont changés aussi ? Pas beaucoup d'info, même dans la doc à ce sujet. Je n'ai jamais eu l'occasion encore d'essayer un virus sur ce mode.
[citation]Le La 432 (ou 444, ou 415, ou autres), j'ai déjà donné mon avis dessus.[/citation]
Moi je l'aime bien! Mais je voulais surtout ici (et c'est la dernière fois que je me répète!) expliquer dans quel contexte le LA 432 Hz trouve sa signification. Soit avec la gamme de pythagore (ou d'autres gammes proches). Trop souvent sur les forums on parle de "détuner" les oscillateurs de synth de -32 cents ou de "détunner" les cordes de guitares pour jouer en LA/432 Hz.... mais on oublie de parler du rapport entre chaque note ou chaque frette de guitare qui n'est pas constant comme la gamme chromatique tempérée. Ça ne suffit pas de simplement ajuster son instrument de quelques Hz. Ni de convertir une chanson .mp3 de 440 à 432......
[citation]On trouve aussi mention du fait que suivant la teneur en minéraux, la pression, la température, et quelques autres choses, ces fréquences de résonances moléculaires varient....
Qu'est-ce qu'on fait du coup : on réaccorde notre La si écoute de la musique en altitude ? [/citation]
je pense que oui! haha! Juste quelques mètres de différences affecte déjà la perception de la hauteur (Hz).
Pour l'eau j'ai déjà essayé de lui envoyer du 432 Hz mais je n'avais pas l'amplitude nécessaire (ou le support adéquat, une plaque de vitre de 0.5 mm d'épaisseur ici) pour la faire vibrer. Et je n'ai pas poussé plus loin.
Je pense que lorsque qu'on se lance dans ce genres d'expériences, il est bon de commencer par des tests très simples.
J'ai commencé par reproduire les figures de chladni. C'est vraiment facile. Même dans des conditions un peu bordeliques, ça fonctionne. Cependant j'ai vite remarqué qu'aussitot que je bouge mes enceintes, le support avec le sel, sa dimension, etc... je dois toujours réajuster la fréquence pour obtenir la même forme...
J'ai fais des tests de lévitation avec de petits objets en métal aussi. Et là ça fonctionnait le soir... mais pu le matin, sans que je ne change rien .... c'est alors que j'ai réalisé que comme pour les figures de chladni, dans l'espace qui nous entoure, il y a des endroits qui vibrent constamment et d'autres endroits des noeuds. Aussi que ces formes varient avec Dame Nature. Autrement dit, qu'il faut toujours réajuster la fréquence de résonance.
Je m'excuse ... on est peut-être pas dans la bonne partie du forum pour discuter de tout ce qui s'éloigne de la musique proprement dit. On peut créer un nouveau sujet dans une section + adéquate si ça intéresse quelqu'un???
ce n'est pas nécessairement tous les instruments qui seront "détuné". Exemple l'accord plaqué du gros pad l'est, mais pas le lead principal.
[citation]j'utilise les différents modes de tuning du virus : tempered, natural ou pure. [/citation]
je pensais qu'il fallait tout changer l'OS à chaque fois pour faire ce genre de manip avec le virus ?? Tu peux me dire si les valeurs (Hz) du filtre et EQ sont changés aussi ? Pas beaucoup d'info, même dans la doc à ce sujet. Je n'ai jamais eu l'occasion encore d'essayer un virus sur ce mode.
[citation]Le La 432 (ou 444, ou 415, ou autres), j'ai déjà donné mon avis dessus.[/citation]
Moi je l'aime bien! Mais je voulais surtout ici (et c'est la dernière fois que je me répète!) expliquer dans quel contexte le LA 432 Hz trouve sa signification. Soit avec la gamme de pythagore (ou d'autres gammes proches). Trop souvent sur les forums on parle de "détuner" les oscillateurs de synth de -32 cents ou de "détunner" les cordes de guitares pour jouer en LA/432 Hz.... mais on oublie de parler du rapport entre chaque note ou chaque frette de guitare qui n'est pas constant comme la gamme chromatique tempérée. Ça ne suffit pas de simplement ajuster son instrument de quelques Hz. Ni de convertir une chanson .mp3 de 440 à 432......
[citation]On trouve aussi mention du fait que suivant la teneur en minéraux, la pression, la température, et quelques autres choses, ces fréquences de résonances moléculaires varient....
Qu'est-ce qu'on fait du coup : on réaccorde notre La si écoute de la musique en altitude ? [/citation]
je pense que oui! haha! Juste quelques mètres de différences affecte déjà la perception de la hauteur (Hz).
Pour l'eau j'ai déjà essayé de lui envoyer du 432 Hz mais je n'avais pas l'amplitude nécessaire (ou le support adéquat, une plaque de vitre de 0.5 mm d'épaisseur ici) pour la faire vibrer. Et je n'ai pas poussé plus loin.
Je pense que lorsque qu'on se lance dans ce genres d'expériences, il est bon de commencer par des tests très simples.
J'ai commencé par reproduire les figures de chladni. C'est vraiment facile. Même dans des conditions un peu bordeliques, ça fonctionne. Cependant j'ai vite remarqué qu'aussitot que je bouge mes enceintes, le support avec le sel, sa dimension, etc... je dois toujours réajuster la fréquence pour obtenir la même forme...
J'ai fais des tests de lévitation avec de petits objets en métal aussi. Et là ça fonctionnait le soir... mais pu le matin, sans que je ne change rien .... c'est alors que j'ai réalisé que comme pour les figures de chladni, dans l'espace qui nous entoure, il y a des endroits qui vibrent constamment et d'autres endroits des noeuds. Aussi que ces formes varient avec Dame Nature. Autrement dit, qu'il faut toujours réajuster la fréquence de résonance.
Je m'excuse ... on est peut-être pas dans la bonne partie du forum pour discuter de tout ce qui s'éloigne de la musique proprement dit. On peut créer un nouveau sujet dans une section + adéquate si ça intéresse quelqu'un???
Pour les figures de chladni, la répartitions des nodes étant une simple histoire de géométrie, il est tout à fait normal d'avoir à réajuster la fréquence quand on change par exemple, sa dimension. C'est d'ailleurs la même chose qui se passe dans une pièce sur les résonances modales, qui déterminent des zones spécifiques de boost et de trous. Change la taille de la pièce, et cela change la fréquence de ces résonances.
D'ailleurs autre chose, quand on parle de résonance mécanique, c'est la fréquence de résonance qui importe, pas des diviseurs ou multiples. C'est d'ailleurs ce qui est utilisé en acoustique pour isoler un sol flottant : on s'assure que la résonance du système sur ressorts ou autres matériaux du genre se retrouve dans les 5-8 Hz, ce qui garanti qu'à partir de 20 Hz, on obtient un découplage très performant. Supposons que la fréquence de résonance du sol soit à 10 Hz, et bien une onde a 80 Hz qui tapera le sol ne fera rien de spécial, même si 80Hz est une harmonique de 10 Hz.
Du coup même si tout le blabla du 432 était cohérent, il n'y aurait que ton La4 qui ferait des choses voodoos sur l'eau, et aucun autre La.
voilà une courbe typique de résonance mécanique en fonction de la fréquence du stimulis :

Comme tu le vois, il n'y a pas d'harmoniques. Dans un cas plus complexe comme de l'eau, tu auras une somme de différentes fréquences (certainement pas multiples ou diviseurs les unes des autres) qui sont liées à la forme moléculaire, cf petit schéma ci-dessous.
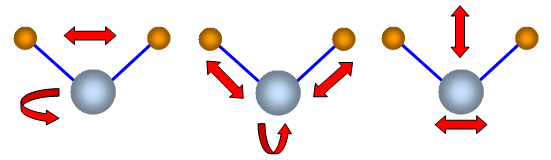
Je n'ai rien contre le fait d'utiliser le La à 432. D'ailleurs peu importe, ce n'est qu'une question de norme arbitraire qui a été posé à 440, donc on peut bien utiliser ce que l'on veut.
Pour le 432 tu peux l'utiliser si tu trouves que s'accorder un peu plus bas c'est plus sympa, mais pas besoin de chercher des justifications cosmiques. Et pour le moment, tous les articles sur le 432 sont abracadabrantesques et ou en mode théorie du complot. Certes c'est marrant de voir la gymnastique des chiffres et on peut les faire se retrouver n'importe où. Ça me fait penser à ce film, le nombre 23 !
Maintenant le sujet de la gamme pythagoricienne est différent, car c'est un choix à faire et celui ci pour le coup n'a rien de voodoo : on choisit entre se taper une grosse quinte fausse à un endroit (qu'on peut éviter d'utiliser) ou se taper des quintes légèrement fausses partout et ne pas avoir de restrictions sur certaines notes. Ou alors même mélanger les deux Tout dépendra du contexte d'utilisation.
Tout dépendra du contexte d'utilisation.
Sinon j'avoue ne pas saisir la question sur l'histoire de la fréquence du filtre et des EQ sur le virus. Un filtre ou un EQ n'est pas quelque chose qui agit sur une fréquence précise mais sur une bande de fréquences (en général encore plus large quand on regarde la phase). Mais si tu as besoin d'être rassuré, tu peux utiliser le keyfollow et donc savoir que celui ci est calé sur des notes, qui peuvent être en mode "pure".
Pour le tuning du virus, c'est un paramètre dans la config sytème, que tu peux bouger en temps réel et entendre ton accord se tuner/detuner.
D'ailleurs autre chose, quand on parle de résonance mécanique, c'est la fréquence de résonance qui importe, pas des diviseurs ou multiples. C'est d'ailleurs ce qui est utilisé en acoustique pour isoler un sol flottant : on s'assure que la résonance du système sur ressorts ou autres matériaux du genre se retrouve dans les 5-8 Hz, ce qui garanti qu'à partir de 20 Hz, on obtient un découplage très performant. Supposons que la fréquence de résonance du sol soit à 10 Hz, et bien une onde a 80 Hz qui tapera le sol ne fera rien de spécial, même si 80Hz est une harmonique de 10 Hz.
Du coup même si tout le blabla du 432 était cohérent, il n'y aurait que ton La4 qui ferait des choses voodoos sur l'eau, et aucun autre La.
voilà une courbe typique de résonance mécanique en fonction de la fréquence du stimulis :

Comme tu le vois, il n'y a pas d'harmoniques. Dans un cas plus complexe comme de l'eau, tu auras une somme de différentes fréquences (certainement pas multiples ou diviseurs les unes des autres) qui sont liées à la forme moléculaire, cf petit schéma ci-dessous.

Je n'ai rien contre le fait d'utiliser le La à 432. D'ailleurs peu importe, ce n'est qu'une question de norme arbitraire qui a été posé à 440, donc on peut bien utiliser ce que l'on veut.
Pour le 432 tu peux l'utiliser si tu trouves que s'accorder un peu plus bas c'est plus sympa, mais pas besoin de chercher des justifications cosmiques. Et pour le moment, tous les articles sur le 432 sont abracadabrantesques et ou en mode théorie du complot. Certes c'est marrant de voir la gymnastique des chiffres et on peut les faire se retrouver n'importe où. Ça me fait penser à ce film, le nombre 23 !
Maintenant le sujet de la gamme pythagoricienne est différent, car c'est un choix à faire et celui ci pour le coup n'a rien de voodoo : on choisit entre se taper une grosse quinte fausse à un endroit (qu'on peut éviter d'utiliser) ou se taper des quintes légèrement fausses partout et ne pas avoir de restrictions sur certaines notes. Ou alors même mélanger les deux
 Tout dépendra du contexte d'utilisation.
Tout dépendra du contexte d'utilisation.Sinon j'avoue ne pas saisir la question sur l'histoire de la fréquence du filtre et des EQ sur le virus. Un filtre ou un EQ n'est pas quelque chose qui agit sur une fréquence précise mais sur une bande de fréquences (en général encore plus large quand on regarde la phase). Mais si tu as besoin d'être rassuré, tu peux utiliser le keyfollow et donc savoir que celui ci est calé sur des notes, qui peuvent être en mode "pure".
Pour le tuning du virus, c'est un paramètre dans la config sytème, que tu peux bouger en temps réel et entendre ton accord se tuner/detuner.
 super interessant tout ça!
super interessant tout ça![nom]xoC[/nom Certes c'est marrant de voir la gymnastique des chiffres et on peut les faire se retrouver n'importe où. Ça me fait penser à ce film, le nombre 23 !
hehe moi chuis mega cartesien a la base pourtant a donf ds le 23. J'invite juste au passage a plutôt voir le film "23" de 1998 de hanz christan schmid sur le hacker Karl Koch plutôt que le film 'le nombre 23' avec jim carey, que je trouve d'une nulité sans nom perso. mais wé ça va etre hors sujet^^.. quoique les 2 films sont une sorte de warning au numero mysticisme
et ce genre de linens foireux, la synchronicité ect..
pour revenir sur le sujet, je sais pas ptet jme plante totalement mais
Ya un autre truc auquel j'ai pensé c que tous les supports actuels, moteur audio ect exports/mastering se font aussi sur la "grille" 44k.1, donc quelque part un CD par exemble,
est 'calibré' en La 440, dans ses derniers retranchements il aura plus de facilité a reproduire fidelement un la 440 a 22khz car aligné sur sa grille qu'a 432 ou il y aura des interference et une plus grande degratdation du signal.' quelque part le la440 est la note qui profitera le mieux de la matrice 44.1, aura la meilleure resolution sans artefacts.
EDIT: non g tout faux en fait, 44100 est un F10, detuné de 23 pourcents ^^
Waa c'est la première fois que je lis des trucs vraiment intéressants à ce sujet... !
Là c'est vraiment instructif, même si c'est un peu dur de vous suivre sur certains trucs K b K et xoc, mais vous donnez de vraies pistes de recherche loin des trucs mystiques qu'on lit habituellement....
[citation]ou se taper des quintes légèrement fausses partout [/citation]
Mais alors, les histoires d'oreille absolue c'est de la foutaise aussi ?!
J'ai souvent lu des récits de types ayant prétendument cette fameuse oreille absolue, qui disaient ne pas pouvoir supporter un instrument même très légèrement faux, voire même ne pas parvenir à écouter des instruments qui ne donnent pas la note exacte que celle jouée, comme certains instruments à vent...
[citation]Citation AF
Je confirme ... ma soeur avait l'oreille absolue (comme moi - l'hérédité doit quand même avoir un rôle !) ... au bout de 6 mois de solfège elle reconnaissait spontanément n'importe quelle note sur mon piano.
Puis elle s'est mise à la trompette (sib) ... et ca a tout embrouillé
Pour ceux qui ne connaissent pas, quand on joue un "do" sur un instrument en sib ... c'est en fait un sib qui sort.
Son prof m'avait proposé d'apprendre le tuba (sib aussi), j'ai fait un cours, j'ai failli devenir fou[/citation]
...
Ou alors ça voudrait dire qu'ils auraient calibré leur oreille au fil de leur apprentissage du solfège, et que ayant totalement intégré les hauteurs découlant du LA440, le reste ne passe plus ?!
En gros les types qui ont l'oreille absolue l'ont pour la fréquence de référence qu'ils ont apprise... ?
Du coup les "absolutistes" qui ont appris le 440hz trouveront forcément le 432 insupportable, et inversement... Et celui qui aurait appris par exemple que le LA vaut 443hz trouvera également que ni le 440 ni le 432 ne sonne juste... ?? A ce moment là, exit les histoires de musiques plus en adéquation avec le corps et la nature pour eux...
A moins que j'ai tout compris de travers, je trouve ça bizarre toute cette histoire, j'attends vos lumières...
Désolé de sortir un peu du sujet... mais ça peut aussi aider à démystifier tout ça !!
Là c'est vraiment instructif, même si c'est un peu dur de vous suivre sur certains trucs K b K et xoc, mais vous donnez de vraies pistes de recherche loin des trucs mystiques qu'on lit habituellement....
[citation]ou se taper des quintes légèrement fausses partout [/citation]
Mais alors, les histoires d'oreille absolue c'est de la foutaise aussi ?!
J'ai souvent lu des récits de types ayant prétendument cette fameuse oreille absolue, qui disaient ne pas pouvoir supporter un instrument même très légèrement faux, voire même ne pas parvenir à écouter des instruments qui ne donnent pas la note exacte que celle jouée, comme certains instruments à vent...
[citation]Citation AF
Je confirme ... ma soeur avait l'oreille absolue (comme moi - l'hérédité doit quand même avoir un rôle !) ... au bout de 6 mois de solfège elle reconnaissait spontanément n'importe quelle note sur mon piano.
Puis elle s'est mise à la trompette (sib) ... et ca a tout embrouillé
Pour ceux qui ne connaissent pas, quand on joue un "do" sur un instrument en sib ... c'est en fait un sib qui sort.
Son prof m'avait proposé d'apprendre le tuba (sib aussi), j'ai fait un cours, j'ai failli devenir fou[/citation]
...
Ou alors ça voudrait dire qu'ils auraient calibré leur oreille au fil de leur apprentissage du solfège, et que ayant totalement intégré les hauteurs découlant du LA440, le reste ne passe plus ?!
En gros les types qui ont l'oreille absolue l'ont pour la fréquence de référence qu'ils ont apprise... ?
Du coup les "absolutistes" qui ont appris le 440hz trouveront forcément le 432 insupportable, et inversement... Et celui qui aurait appris par exemple que le LA vaut 443hz trouvera également que ni le 440 ni le 432 ne sonne juste... ?? A ce moment là, exit les histoires de musiques plus en adéquation avec le corps et la nature pour eux...
A moins que j'ai tout compris de travers, je trouve ça bizarre toute cette histoire, j'attends vos lumières...

Désolé de sortir un peu du sujet... mais ça peut aussi aider à démystifier tout ça !!
c pas du tout hors sujet c exactement la question que je me posait page d'avant a savoir si l'ecoute "tonale" est physique/absolue ou culturelle,
en ce cas wé tout ça ne voudrait rien dire. et a priori ça...:
from wikipedia 'oreille absolue':
en ce cas wé tout ça ne voudrait rien dire. et a priori ça...:
from wikipedia 'oreille absolue':
Wikipedia wrote :
Il est cependant nécessaire de préciser que les musiciens dotés de l'oreille absolue, active comme passive, peuvent être désavantagés lorsqu'il s'agit, comme c'est le cas au cours d'examens dans les écoles de musique et conservatoires, de prendre une « dictée musicale » dans laquelle le diapason change. En effet, le diapason de référence étant le La dit « La 440 » (442 pour l'orchestre) - c'est-à-dire une fréquence de 440 (442 pour l'orchestre) vibrations par seconde - lorsque, par exemple, un morceau de musique baroque, c'est-à-dire en « La 415 », est donné en dictée, l'oreille absolue se retrouve en décalage par rapport aux sons émis. Dans ce cas, elle ne sert plus à rien, et constitue même un handicap pour le musicien. Cependant ce type d'exercice est rare, et le "diapason baroque" qui serait à 415 est aujourd'hui sérieusement remis en question par les musicologues. Dans tous les autres cas de dictée où le diapason du 440 Hz est respecté, l'oreille absolue est un avantage immense.
oui l'oreille absolu c'est finalement juste une capacité à associer très rapidement (et facilement) une fréquence avec une note (un mot quoi...). Quelqu'un qui a cette compétence pourra du coup se réadapter, avec un peu d'effort, à un autre référentiel.
Finalement, ce que je retiens surtout de Pythagore et consort, c'est que la fréquence D'UNE note n'est pas tellement importante. C'est bien plus les INTERVALLES entre les notes, la proportion des écarts, qui va tout faire.
Comme d'hab quoi
Finalement, ce que je retiens surtout de Pythagore et consort, c'est que la fréquence D'UNE note n'est pas tellement importante. C'est bien plus les INTERVALLES entre les notes, la proportion des écarts, qui va tout faire.
Comme d'hab quoi

carement, ça enleve rien a l'idee des ratios/intervalles.
mais pour les 432istes^^ on est d'accord que 90 pourcent des occidentaux sont "formatés" et ont développé leur systeme d'écoute/mémoire tonale sur le systeme 440 Hz, et dc a priori trouveront forcement un accordage different un peu chelou..
mais pour les 432istes^^ on est d'accord que 90 pourcent des occidentaux sont "formatés" et ont développé leur systeme d'écoute/mémoire tonale sur le systeme 440 Hz, et dc a priori trouveront forcement un accordage different un peu chelou..
Oui, quelqu'un avec l'oreille absolue va être un peu agressé par les accordages différents. Mais il y a différents degrés d'oreille absolue, concernant l'écart tolérable.
Sinon la plupart des gens ont une oreille dite relative, c'est à dire que le cerveau imprime les écarts par rapport à une référence donnée, et non innée. Du coup si tu leur fais écouter un La 432 le matin, et joue derrière accordé en 432 cela ne les gênera pas du tout.
Après certains instruments sont bloqués dans leur accordage : piano, guitare avec fret, etc.
Je me rappelle, ayant fait 10 ans de violon étant plus jeune, que l'on ne jouait pas un Fa dièse et un Sol bémol à la même hauteur : un demi ton se partageait de 9 comma, et un dièse se jouait avec 4 comma de +, un bémol 4 de moins, ce qui donnait un écart d'un comma entre les deux.
En fait, avec tous les instruments dont la hauteur est modulable à souhait, c'est un peu une mixture de tous ces types d'accordage que l'on utilise, en temps réel, à l'oreille, selon ce qui sonne le mieux, ainsi que de désaccorder sciemment, pour créer plus de tension/émotions sur les altérations. Cela peut aussi dépendre du répertoire (classique vs moderne/contemporain par exemple)
Sinon la plupart des gens ont une oreille dite relative, c'est à dire que le cerveau imprime les écarts par rapport à une référence donnée, et non innée. Du coup si tu leur fais écouter un La 432 le matin, et joue derrière accordé en 432 cela ne les gênera pas du tout.
Après certains instruments sont bloqués dans leur accordage : piano, guitare avec fret, etc.
Je me rappelle, ayant fait 10 ans de violon étant plus jeune, que l'on ne jouait pas un Fa dièse et un Sol bémol à la même hauteur : un demi ton se partageait de 9 comma, et un dièse se jouait avec 4 comma de +, un bémol 4 de moins, ce qui donnait un écart d'un comma entre les deux.
En fait, avec tous les instruments dont la hauteur est modulable à souhait, c'est un peu une mixture de tous ces types d'accordage que l'on utilise, en temps réel, à l'oreille, selon ce qui sonne le mieux, ainsi que de désaccorder sciemment, pour créer plus de tension/émotions sur les altérations. Cela peut aussi dépendre du répertoire (classique vs moderne/contemporain par exemple)
a wé ok c ouf moi jme disais que vu qu'on ecoutait 90 pourcent de zik en 440, notre cerveau se calibrait en quelque sorte 'naturellement' dessus
comme reference. j'ai appris quelque chose ajd
comme reference. j'ai appris quelque chose ajd
[citation]Du coup même si tout le blabla du 432 était cohérent, il n'y aurait que ton La4 qui ferait des choses voodoos sur l'eau, et aucun autre La.[/citation]
En effet, lorsque je recherche les différentes fréquences de résonance d'une matière, ça arrive parfois que je retrouve des harmoniques, mais jamais un rapport d'octave (pour ma part).
[citation]Pour le 432 tu peux l'utiliser si tu trouves que s'accorder un peu plus bas c'est plus sympa, mais pas besoin de chercher des justifications cosmiques.[/citation]
Oui, pour la plupart des gens c'est simplement un effet placebo!
[citation]Certes c'est marrant de voir la gymnastique des chiffres et on peut les faire se retrouver n'importe où. Ça me fait penser à ce film, le nombre 23 ![/citation]
Hehe, j'aime pas trop la gymnastique des chiffres moi non + en général. Mais petit détail intéressant que je n'ai pas vu ailleur : C'est la somme de l'addition des chiffres d'une note dans le tableau que j'ai posté plus haut. Toujours 9 (sauf pour SOL, 3 et 6 successivement).
[citation]Maintenant le sujet de la gamme pythagoricienne est différent, car c'est un choix à faire et celui ci pour le coup n'a rien de voodoo[/citation]
Considérent l'intêret de Pythagore pour les nombres entier... ca donne un joli tableau avec un LA-432! Mise à part LA en 432 Hz, pas d'autre tableau donne autant de nombre entier. Et le triangle 3,4,5 de pythagore y trouve un sens aussi.
EDIT : je voulais rajouter que les valeurs des notes sont calculées avec les raports de nombres entiers les plus petits. Comme on peut voir (colonne à droite) sur ma photo + haut.
[citation]Ou alors même mélanger les deux [/citation]
[/citation]
J'ai fais ça la semaine dernière! Une version pour chaque mode et une dans les 2. Voici un extrait, celle qui mélange les 2. La quinte est en pythagoricen et la mélodie par dessus en chromatique tempérée. Enregistré sur android mais on entend bien la quinte en mode pythagorien Ça crève les oreilles. Pour la mélodie, c'est + substile.
http://youtu.be/t8W2wi0h9nA?t=1m18s
(désolé, pour ma tenue matinal et le bordel de mes rénos)
[citation]Sinon j'avoue ne pas saisir la question sur l'histoire de la fréquence du filtre et des EQ sur le virus.[/citation]
En général, la plage de fréquence est répartie sur les valeurs MIDI (0-127). Chacune de ces valeurs correspond à une fréquence associé au "tunning" de la gamme chromatique tempéré. Quand je mets un filtre en mode "self oscilate" (résonance à fond, 127) je peux visionner la fréquence de coupure sur un analyseur de spectre. Bien sur cette fréquence peut varier selon la pente et le mode du filtre, mais c'est souvent très près ou exactement sur les Hz associés à la gamme chromatique tempérée.
Pourquoi je demande ça ? car j'ai remarqué encore une énorme différence sur le son après avoir créer un filtre adapté à la gamme avec mon synthé. Des trucs impossible à recréer autrement. À moins d'utiliser un filtre avec une résolution + grande s'il n'est pas "tunné" sur la gamme utilisée.
[citation]Mais si tu as besoin d'être rassuré, tu peux utiliser le keyfollow[/citation]
Non justement, car dans mon cas, j'ai associé une valeur de Hz pour chaque note MIDI ... mais la fonction keyfollow est toujours ajusté sur le mode chromatique tempéré. Et dans d'autres circonstance d'utilisation la fonction keyfollow n'aide pas.
[citation]Ya un autre truc auquel j'ai pensé c que tous les supports actuels, moteur audio ect exports/mastering se font aussi sur la "grille" 44k.1, donc quelque part un CD par exemble,[/citation]
Pour ma part j'opterais pour 52 800 Hz
[citation]c'est que la fréquence D'UNE note n'est pas tellement importante. C'est bien plus les INTERVALLES entre les notes, la proportion des écarts, qui va tout faire.[/citation]
Je reprendrais ce que je disais + haut à ce sujet. Aussi dépendant de la recette que tu veux faire, chaque ingrédient est important.
Hey Xoc ?! tu n'avais pas l'oreille absolue toi (p.s. te gène pas pour me dire si je t'interpelle trop dans la discussion!) Parlant de violon j'avais lu que le stradivarius était accordé en 432... détail que je n'ai jamais pris le temps de vérifier moi même encore.
En effet, lorsque je recherche les différentes fréquences de résonance d'une matière, ça arrive parfois que je retrouve des harmoniques, mais jamais un rapport d'octave (pour ma part).
[citation]Pour le 432 tu peux l'utiliser si tu trouves que s'accorder un peu plus bas c'est plus sympa, mais pas besoin de chercher des justifications cosmiques.[/citation]
Oui, pour la plupart des gens c'est simplement un effet placebo!
[citation]Certes c'est marrant de voir la gymnastique des chiffres et on peut les faire se retrouver n'importe où. Ça me fait penser à ce film, le nombre 23 ![/citation]
Hehe, j'aime pas trop la gymnastique des chiffres moi non + en général. Mais petit détail intéressant que je n'ai pas vu ailleur : C'est la somme de l'addition des chiffres d'une note dans le tableau que j'ai posté plus haut. Toujours 9 (sauf pour SOL, 3 et 6 successivement).
[citation]Maintenant le sujet de la gamme pythagoricienne est différent, car c'est un choix à faire et celui ci pour le coup n'a rien de voodoo[/citation]
Considérent l'intêret de Pythagore pour les nombres entier... ca donne un joli tableau avec un LA-432! Mise à part LA en 432 Hz, pas d'autre tableau donne autant de nombre entier. Et le triangle 3,4,5 de pythagore y trouve un sens aussi.
EDIT : je voulais rajouter que les valeurs des notes sont calculées avec les raports de nombres entiers les plus petits. Comme on peut voir (colonne à droite) sur ma photo + haut.
[citation]Ou alors même mélanger les deux
 [/citation]
[/citation]J'ai fais ça la semaine dernière! Une version pour chaque mode et une dans les 2. Voici un extrait, celle qui mélange les 2. La quinte est en pythagoricen et la mélodie par dessus en chromatique tempérée. Enregistré sur android mais on entend bien la quinte en mode pythagorien Ça crève les oreilles. Pour la mélodie, c'est + substile.
http://youtu.be/t8W2wi0h9nA?t=1m18s
(désolé, pour ma tenue matinal et le bordel de mes rénos)
[citation]Sinon j'avoue ne pas saisir la question sur l'histoire de la fréquence du filtre et des EQ sur le virus.[/citation]
En général, la plage de fréquence est répartie sur les valeurs MIDI (0-127). Chacune de ces valeurs correspond à une fréquence associé au "tunning" de la gamme chromatique tempéré. Quand je mets un filtre en mode "self oscilate" (résonance à fond, 127) je peux visionner la fréquence de coupure sur un analyseur de spectre. Bien sur cette fréquence peut varier selon la pente et le mode du filtre, mais c'est souvent très près ou exactement sur les Hz associés à la gamme chromatique tempérée.
Pourquoi je demande ça ? car j'ai remarqué encore une énorme différence sur le son après avoir créer un filtre adapté à la gamme avec mon synthé. Des trucs impossible à recréer autrement. À moins d'utiliser un filtre avec une résolution + grande s'il n'est pas "tunné" sur la gamme utilisée.
[citation]Mais si tu as besoin d'être rassuré, tu peux utiliser le keyfollow[/citation]
Non justement, car dans mon cas, j'ai associé une valeur de Hz pour chaque note MIDI ... mais la fonction keyfollow est toujours ajusté sur le mode chromatique tempéré. Et dans d'autres circonstance d'utilisation la fonction keyfollow n'aide pas.
[citation]Ya un autre truc auquel j'ai pensé c que tous les supports actuels, moteur audio ect exports/mastering se font aussi sur la "grille" 44k.1, donc quelque part un CD par exemble,[/citation]
Pour ma part j'opterais pour 52 800 Hz
[citation]c'est que la fréquence D'UNE note n'est pas tellement importante. C'est bien plus les INTERVALLES entre les notes, la proportion des écarts, qui va tout faire.[/citation]
Je reprendrais ce que je disais + haut à ce sujet. Aussi dépendant de la recette que tu veux faire, chaque ingrédient est important.
Hey Xoc ?! tu n'avais pas l'oreille absolue toi (p.s. te gène pas pour me dire si je t'interpelle trop dans la discussion!) Parlant de violon j'avais lu que le stradivarius était accordé en 432... détail que je n'ai jamais pris le temps de vérifier moi même encore.
[citation]Hehe, j'aime pas trop la gymnastique des chiffres moi non + en général. Mais petit détail intéressant que je n'ai pas vu ailleur : C'est la somme de l'addition des chiffres d'une note dans le tableau que j'ai posté plus haut. Toujours 9 (sauf pour SOL, 3 et 6 successivement).
[/citation]
et alors ?
[citation]Considérent l'intêret de Pythagore pour les nombres entier... ca donne un joli tableau avec un LA-432! Mise à part LA en 432 Hz, pas d'autre tableau donne autant de nombre entier. Et le triangle 3,4,5 de pythagore y trouve un sens aussi.[/citation]
Sauf que cette notion de nombre entier en parlant de fréquence n'avait aucun sens avant que la valeur de la seconde soit unifiée en 1967, et je re-cite ce que j'ai mis plus haut : "La seconde de temps est la durée de 9 192 631 770 périodes d'un rayonnement particulier émis par le césium 133".
Se caler sur une fréquence entière nous fait une belle jambe tiens donc.
Je t'épargne le calcul si tu veux trouver quelque chose de voodoo dans le cesium : ce nombre se décompose comme suit : 2 x 3 x 3 x 5 × 7 x 7 × 47 × 44351.
[citation]En général, la plage de fréquence est répartie sur les valeurs MIDI (0-127). Chacune de ces valeurs correspond à une fréquence associé au "tunning" de la gamme chromatique tempéré. Quand je mets un filtre en mode "self oscilate" (résonance à fond, 127) je peux visionner la fréquence de coupure sur un analyseur de spectre. Bien sur cette fréquence peut varier selon la pente et le mode du filtre, mais c'est souvent très près ou exactement sur les Hz associés à la gamme chromatique tempérée.
Pourquoi je demande ça ? car j'ai remarqué encore une énorme différence sur le son après avoir créer un filtre adapté à la gamme avec mon synthé. Des trucs impossible à recréer autrement. À moins d'utiliser un filtre avec une résolution + grande s'il n'est pas "tunné" sur la gamme utilisée.[/citation]
Plusieurs choses :
- la plus haute note midi a une fréquence relativement basse : 12 kHz. heureusement que les filtres ne sont pas calés dessus !
- les plages de valeurs midi sur les synths hardware ont certes une valeur fixe de 0 à 127 (encore que certains utilisent en interne une valeur sysex plus précise), et la formule est simple à calculer : on fait une bijection exponentielle en base 2 (une fonction de type a*2^(b*x+c)) en choisissant bien les constantes a, b et c pour que la fonction bijecte de [0;127] dans [20;20000] par exemple, ou autre valeurs si l'on veut une étendue plus grande/petite sur la fréquence du filtre. y'a donc aucune chance que l'on se mappe pile dessus la gamme chromatique. Mais oui j'ai déjà vu certains synthés et EQ, où ils s'amusent à dire à quelle note de la gamme chromatique cela correspond, mais c'est loin d'être la majorité.
- les synths en vsti utilisent une valeur du filtre généralement codée en 32 bits float (voir 64 pour ceux qui tournent en précision double).
- j'ai jamais un seul patch de synth avec un filtre statique.
- la fréquence de coupure que tu vas pouvoir déduire d'un analyseur de spectre : un analyseur classique avec 8000 samples de buffer pour la taille d'analyse va avoir une résolution fréquentielle de +/- 5 Hz sur tout le spectre. Si tu utilises des buffers bcp + gros pour plus de résolution, tu va perdre énormément en résolution temporelle, et il te faut des echantillons statiques, très longs, si tu veux que cette précision sur la fréquence ait un sens.
On remarque d'ailleurs souvent que les analyseurs à base de transformée de fourier (c'est à dire à peu près tous) à partir de 16000 bloc et plus commencent à mettre des ptits pics de fréquences qui n'existent pas entre certaines harmoniques de la basse par exemple, justement parce que l'échantillon n'est pas statique.
On peut avoir plus de précision avec des wavelets, mais elles ont aussi d'autres compromis.
Donc déduire à vu d'oeil sur un analyseur de spectre que le filtre est exactement sur une fréquence de la gamme chromatique ...
Sachant aussi que la fréquence d'un filtre n'est qu'une convention : on a choisit pour la plupart le point auquel le filtre bouffe 3 dB, par pure convention. Et certains filtres s'expriment avec des points à -6 dB (par exemple les filtres Linkwitz-Riley utilisés dans les cross-over des enceintes).
Pourquoi -3 et -6 ? là aussi c'est une approximation et une convention qui nous arrange : diviser par deux l'amplitude correspond à peu près à -6.02 dB, et diviser l'amplitude par racine de de 2 correspond à peu près à -3.01 dB, mais c'est encore approximé ici, pour ceux que cela intéresse plus, un ptit lien en anglais avec plus de chiffres après la virgule :
http://hbfs.wordpress.com/2008/12/09/deriving-the-1-bit-6-db-rule-of-thumb/
[citation]Non justement, car dans mon cas, j'ai associé une valeur de Hz pour chaque note MIDI ... mais la fonction keyfollow est toujours ajusté sur le mode chromatique tempéré. Et dans d'autres circonstance d'utilisation la fonction keyfollow n'aide pas.[/citation]
Un key follow bien programmé va suivre le pitch total : c'est à dire midi note + fine tune. D'ailleurs les effets midi qui permettent de décaler une gamme (pour créer toute sortes de gammes différentes, dont notamment des gammes indiennes avec leur quarts de tons par exemple) fonctionnent souvent comme cela : ils envoient une note midi + un décalage de fine tune via le pitch bend par exemple. Il faut dans ce cas régler le synth pour que le pitchbend soit sur une amplitude de +/- 1 demiton
[citation]Pour ma part j'opterais pour 52 800 Hz[/citation]
Je suis assez curieux d'entendre ton explication la dessus
[citation]Hey Xoc ?! tu n'avais pas l'oreille absolue toi (p.s. te gène pas pour me dire si je t'interpelle trop dans la discussion!) Parlant de violon j'avais lu que le stradivarius était accordé en 432...[/citation]
Le stradivarius était accordé sur ce qui se faisait à son époque, c'est à dire plutôt sur le La à 415 hz. D'ailleurs c'est un autre débat, mais des médailles d'or de violon et des experts de violon, en double blind test (3 stradivarius et 3 violons haut de gamme récents) ont été incapables de les départager : ils devaient, sur chaque groupe de test, identifier le violon ancien et le violon récent, ils n'ont pas réussi.
Sinon pour l'oreille absolue, oui, et ça m'a plus souvent gêné qu'autre chose. Mais à force de faire de la psytrance glauque avec des accords dissonants et désaccordés de partout, j'ai un peu augmenté ma tolérance au detuning, et tant mieux !
Et non, ne t'inquiète pas, cela ne me dérange jamais de débattre de son
[/citation]
et alors ?
[citation]Considérent l'intêret de Pythagore pour les nombres entier... ca donne un joli tableau avec un LA-432! Mise à part LA en 432 Hz, pas d'autre tableau donne autant de nombre entier. Et le triangle 3,4,5 de pythagore y trouve un sens aussi.[/citation]
Sauf que cette notion de nombre entier en parlant de fréquence n'avait aucun sens avant que la valeur de la seconde soit unifiée en 1967, et je re-cite ce que j'ai mis plus haut : "La seconde de temps est la durée de 9 192 631 770 périodes d'un rayonnement particulier émis par le césium 133".
Se caler sur une fréquence entière nous fait une belle jambe tiens donc.
Je t'épargne le calcul si tu veux trouver quelque chose de voodoo dans le cesium : ce nombre se décompose comme suit : 2 x 3 x 3 x 5 × 7 x 7 × 47 × 44351.
[citation]En général, la plage de fréquence est répartie sur les valeurs MIDI (0-127). Chacune de ces valeurs correspond à une fréquence associé au "tunning" de la gamme chromatique tempéré. Quand je mets un filtre en mode "self oscilate" (résonance à fond, 127) je peux visionner la fréquence de coupure sur un analyseur de spectre. Bien sur cette fréquence peut varier selon la pente et le mode du filtre, mais c'est souvent très près ou exactement sur les Hz associés à la gamme chromatique tempérée.
Pourquoi je demande ça ? car j'ai remarqué encore une énorme différence sur le son après avoir créer un filtre adapté à la gamme avec mon synthé. Des trucs impossible à recréer autrement. À moins d'utiliser un filtre avec une résolution + grande s'il n'est pas "tunné" sur la gamme utilisée.[/citation]
Plusieurs choses :
- la plus haute note midi a une fréquence relativement basse : 12 kHz. heureusement que les filtres ne sont pas calés dessus !
- les plages de valeurs midi sur les synths hardware ont certes une valeur fixe de 0 à 127 (encore que certains utilisent en interne une valeur sysex plus précise), et la formule est simple à calculer : on fait une bijection exponentielle en base 2 (une fonction de type a*2^(b*x+c)) en choisissant bien les constantes a, b et c pour que la fonction bijecte de [0;127] dans [20;20000] par exemple, ou autre valeurs si l'on veut une étendue plus grande/petite sur la fréquence du filtre. y'a donc aucune chance que l'on se mappe pile dessus la gamme chromatique. Mais oui j'ai déjà vu certains synthés et EQ, où ils s'amusent à dire à quelle note de la gamme chromatique cela correspond, mais c'est loin d'être la majorité.
- les synths en vsti utilisent une valeur du filtre généralement codée en 32 bits float (voir 64 pour ceux qui tournent en précision double).
- j'ai jamais un seul patch de synth avec un filtre statique.
- la fréquence de coupure que tu vas pouvoir déduire d'un analyseur de spectre : un analyseur classique avec 8000 samples de buffer pour la taille d'analyse va avoir une résolution fréquentielle de +/- 5 Hz sur tout le spectre. Si tu utilises des buffers bcp + gros pour plus de résolution, tu va perdre énormément en résolution temporelle, et il te faut des echantillons statiques, très longs, si tu veux que cette précision sur la fréquence ait un sens.
On remarque d'ailleurs souvent que les analyseurs à base de transformée de fourier (c'est à dire à peu près tous) à partir de 16000 bloc et plus commencent à mettre des ptits pics de fréquences qui n'existent pas entre certaines harmoniques de la basse par exemple, justement parce que l'échantillon n'est pas statique.
On peut avoir plus de précision avec des wavelets, mais elles ont aussi d'autres compromis.
Donc déduire à vu d'oeil sur un analyseur de spectre que le filtre est exactement sur une fréquence de la gamme chromatique ...
Sachant aussi que la fréquence d'un filtre n'est qu'une convention : on a choisit pour la plupart le point auquel le filtre bouffe 3 dB, par pure convention. Et certains filtres s'expriment avec des points à -6 dB (par exemple les filtres Linkwitz-Riley utilisés dans les cross-over des enceintes).
Pourquoi -3 et -6 ? là aussi c'est une approximation et une convention qui nous arrange : diviser par deux l'amplitude correspond à peu près à -6.02 dB, et diviser l'amplitude par racine de de 2 correspond à peu près à -3.01 dB, mais c'est encore approximé ici, pour ceux que cela intéresse plus, un ptit lien en anglais avec plus de chiffres après la virgule :
http://hbfs.wordpress.com/2008/12/09/deriving-the-1-bit-6-db-rule-of-thumb/
[citation]Non justement, car dans mon cas, j'ai associé une valeur de Hz pour chaque note MIDI ... mais la fonction keyfollow est toujours ajusté sur le mode chromatique tempéré. Et dans d'autres circonstance d'utilisation la fonction keyfollow n'aide pas.[/citation]
Un key follow bien programmé va suivre le pitch total : c'est à dire midi note + fine tune. D'ailleurs les effets midi qui permettent de décaler une gamme (pour créer toute sortes de gammes différentes, dont notamment des gammes indiennes avec leur quarts de tons par exemple) fonctionnent souvent comme cela : ils envoient une note midi + un décalage de fine tune via le pitch bend par exemple. Il faut dans ce cas régler le synth pour que le pitchbend soit sur une amplitude de +/- 1 demiton
[citation]Pour ma part j'opterais pour 52 800 Hz[/citation]
Je suis assez curieux d'entendre ton explication la dessus
[citation]Hey Xoc ?! tu n'avais pas l'oreille absolue toi (p.s. te gène pas pour me dire si je t'interpelle trop dans la discussion!) Parlant de violon j'avais lu que le stradivarius était accordé en 432...[/citation]
Le stradivarius était accordé sur ce qui se faisait à son époque, c'est à dire plutôt sur le La à 415 hz. D'ailleurs c'est un autre débat, mais des médailles d'or de violon et des experts de violon, en double blind test (3 stradivarius et 3 violons haut de gamme récents) ont été incapables de les départager : ils devaient, sur chaque groupe de test, identifier le violon ancien et le violon récent, ils n'ont pas réussi.
Sinon pour l'oreille absolue, oui, et ça m'a plus souvent gêné qu'autre chose. Mais à force de faire de la psytrance glauque avec des accords dissonants et désaccordés de partout, j'ai un peu augmenté ma tolérance au detuning, et tant mieux !

Et non, ne t'inquiète pas, cela ne me dérange jamais de débattre de son

Bon bah n'ayant rien de constructif à apporter à cette discussion, je me contente de m'installer dans un coin, mais continuez svp c'est passionnant 

la meme pour moi
merci xoc car le délire avec le detune je l'utilisais pour faire de la stéréo
si vous pouviez nous faire un cours ça serais moumoutte
moumoutte
merci xoc car le délire avec le detune je l'utilisais pour faire de la stéréo
si vous pouviez nous faire un cours ça serais
 moumoutte
moumoutte Grin wrote :
Un deuxième lien intéressant où est expliqué le "Tetractys", figure rigolote de Pythagore, évolution fractale du rapport entre les nombres premiers (et du coup, entre les notes de musiques, et les fréquences, aussi).
Tenez commencez par l'intro, c'est franchement intéressant (et uniquement "mathématique" au sens large... à vous de faire vos liens dans votre tête)
http://mathematiquespythagoriciennes.lo.gs/prologue-a46006199
edit : ca me fait délirer, je lis ça et je m'imagine des ptits vieux, en mode jedi qui remplacent la "force" par le nombre, mystico-mathématiciens, je trouve ca trop trippant
J' avais peur de faire un hs en parlant de tétraktys, qui m' a sauté aux yeux au milieu de ta page mathématique en lien, mais puisque tu en parles le premier, j' ai un album à ce nom :
http://www.psyshop.com/shop/CDs/sbr/sbr1cd005.html
J' y avais tout de suite reconnu un mot à consonance grecque. Tétra qui veut dire 4, je crois.
Effectivement, je confirme:
http://fr.wikipedia.org/wiki/T%C3%A9tra-
angelique wrote :
J' avais peur de faire un hs en parlant de tétraktys, qui m' a sauté aux yeux au milieu de ta page mathématique en lien, mais puisque tu en parles le premier, j' ai un album à ce nom :
http://www.psyshop.com/shop/CDs/sbr/sbr1cd005.html
J' y avais tout de suite reconnu un mot à consonance grecque. Tétra qui veut dire 4, je crois.
Effectivement, je confirme:
http://fr.wikipedia.org/wiki/T%C3%A9tra-
si comme presque partout ou tu post

mais bon a fil du temps on s’habitue a toi malheureusement
mais bon la tu nous a excuser le pavé pour raconter ta vie qui nous fatigue pas vraiment a lire mais c'est chiant de devoir jouer toujours avec la souris pour suivre le fil des conversations et devoir sauter a chaque fois tes pavé inintéressant qui parle de toi, et de toi, et de toi et ce que tu pense
merci je dirais
"en progression et fait des efforts"

foxatap wrote :
c tt a fait possible (et mem sur) qu'il y ai des 'résonances' ayant une influence, cosmiques, fréquence de shumman, l'eau, ondes alpha blabla mais a chaque fois c le meme barratin ya aucune source/etude scientifique vraiment sérieuse et crédible, on dit juste "ya une etude scientifique" ac une image jpg et blam on est censé prendre ça pour argent comptant.
Je déteste l' occulte.

Il y a assez de matière avec la science réelle présente et à venir sans aller se laver le cerveau chez les sectes. Tous ces trucs me foutent le mal de mer [:beurk]
djzarro wrote :
si comme presque partout ou tu post
mais bon a fil du temps on s’habitue a toi malheureusement
mais bon la tu nous a excuser le pavé pour raconter ta vie qui nous fatigue pas vraiment a lire mais c'est chiant de devoir jouer toujours avec la souris pour suivre le fil des conversations et devoir sauter a chaque fois tes pavé inintéressant qui parle de toi, et de toi, et de toi et ce que tu pense
merci je dirais
"en progression et fait des efforts"
Je te rassure, pour ma part je n' ai aucune envie de me prendre le chou avec le La 440 Hz

Merci prof, tu me donnes quelle note sur mon carnet trimestriel
 ?
? angelique wrote :
Je te rassure, pour ma part je n' ai aucune envie de me prendre le chou avec le La 440 Hz
Merci prof, tu me donnes quelle note sur mon carnet trimestriel?
merci pour nous

ça taille^^
allez la K-b k revieeent tu px pas dire plein dtrucs et te barrer comme ça!..^^
parles nous du 52800 . qui que quoi dont ou comment
moi aussi ça m'intrigue
allez la K-b k revieeent tu px pas dire plein dtrucs et te barrer comme ça!..^^
parles nous du 52800 . qui que quoi dont ou comment
moi aussi ça m'intrigue
[citation]...Mais petit détail intéressant que je n'ai pas vu ailleur : C'est la somme de l'addition des chiffres d'une note dans le tableau que j'ai posté plus haut. Toujours 9 (sauf pour SOL, 3 et 6 successivement).
et alors ?[/citation]
et alors rien ! Je le mentionne car je n'ai pas vu personne en parler ailleur. Si ca peut aider ceux qui "jonglent" avec les nombres !
Voici comment on calcul :
LA/432 : 4+3+2 = 9 (facile!)
SI/486 : 4+8+6 = 18 , 1 + 8 = 9
SI/3888 : 3+8+8+8 = 27, 2 + 7 = 9
G#/410.0625 : 4+1+0+0+6+2+5 = 18, 1+ 8 = 9
A#/461.3203125 4+6+1+3+2+0+3+1+2+5 = 27, 2+7 = 9
etc...
[citation]Sauf que cette notion de nombre entier en parlant de fréquence n'avait aucun sens avant que la valeur de la seconde soit unifiée en 1967[/citation]
Pythagore utilise les rapports entiers et les proportions. Lorsqu'on pince un monocorde en son centre on obtient un rapport d'octave (1/2) et ainsi de suite. Ce n'est pas calculer en seconde. Si le temps est relatif, les rapports et les proportions ne le sont pas.
[citation]Platon, dans le Timée, décrit comment le Démiurge façonne l'Âme du monde. J.-Fr. Mattéi résume : "Le démiurge va tirer de sa composition finale une structure harmonique suggestive dont les calculs témoignent d'une influence pythagoricienne. Elle est constituée par une double progression géométrique de raison 2 (1, 2, 4, 8) et de raison 3 (1, 3, 9, 27), qu'il est commode de disposer sur un diagramme en forme de lambda majuscule (Λ , selon un schéma que l'on trouve chez Proclus. Cette figure porte, sur chaque côté de l'angle, les nombres respectifs de la série paire et de la série impaire. Le dernier de ces nombres (27) est égal à la somme des six précédents (1 + 2 + 3 + 4 + 8 + 9 = 27)... La progression selon le facteur 2 donne les octaves par doublement successifs des intervalles (1, 2, 4, 8 = Do1, Do2, Do3, Do4...), alors que la progression selon le facteur 3 forme les douzièmes justes (1 = Do, 3 = Sol, 9 = Ré, 27 = La, 81 = Mi, 243 = SI...). On peut alors combler les intervalles musicaux doubles ou triples pour former la gamme complète en s'aidant de deux proportions continues ou 'médiétés', l'une arithmétique (de type 1, 2, 3), l'autre harmonique (de type 3, 4, 6), bien connues des pythagoriciens, en particulier Archytas. L'intervalle des nombres de 1 à 2 sera composé des nombres 1 (Tonique), 4/3 (Quarte), 3/2 (Quinte) et 2 (Octave) ; le ton, dont la valeur est 9/8, se situe entre la quarte et la quinte, puisque 3/2 : 4/3 = 9/8. L'Âme du monde est ainsi composée de cinq tons majeurs égaux entre lesquels est intercalé comme 'reste', leimma, l'intervalle de 256/243 (= 1,053), mesure du demi-ton diatonique de la gamme naturelle de Pythagore, qui est un peu plus faible que notre demi-ton tempéré (16/15 = 1,066)"[/citation]
, selon un schéma que l'on trouve chez Proclus. Cette figure porte, sur chaque côté de l'angle, les nombres respectifs de la série paire et de la série impaire. Le dernier de ces nombres (27) est égal à la somme des six précédents (1 + 2 + 3 + 4 + 8 + 9 = 27)... La progression selon le facteur 2 donne les octaves par doublement successifs des intervalles (1, 2, 4, 8 = Do1, Do2, Do3, Do4...), alors que la progression selon le facteur 3 forme les douzièmes justes (1 = Do, 3 = Sol, 9 = Ré, 27 = La, 81 = Mi, 243 = SI...). On peut alors combler les intervalles musicaux doubles ou triples pour former la gamme complète en s'aidant de deux proportions continues ou 'médiétés', l'une arithmétique (de type 1, 2, 3), l'autre harmonique (de type 3, 4, 6), bien connues des pythagoriciens, en particulier Archytas. L'intervalle des nombres de 1 à 2 sera composé des nombres 1 (Tonique), 4/3 (Quarte), 3/2 (Quinte) et 2 (Octave) ; le ton, dont la valeur est 9/8, se situe entre la quarte et la quinte, puisque 3/2 : 4/3 = 9/8. L'Âme du monde est ainsi composée de cinq tons majeurs égaux entre lesquels est intercalé comme 'reste', leimma, l'intervalle de 256/243 (= 1,053), mesure du demi-ton diatonique de la gamme naturelle de Pythagore, qui est un peu plus faible que notre demi-ton tempéré (16/15 = 1,066)"[/citation]
http://fr.wikipedia.org/wiki/Symbolisme_des_nombres
[citation]dans lequel Platon décrit la fabrication des proportions de l'Âme du Monde par le Démiurge. Ce passage est fondé sur la série numérique 1, 2, 3, 4, 9, 8, 27 — qui correspond à la fusion de la série des premières puissances de 2 (2, 4, 8) et de la série des premières puissances de 3 (3, 9, 27). Or, de cette série, on peut tirer les rapports numériques sur lesquels sont fondés les intervalles musicaux : le rapport de 1 à 2 (rapport double) correspond à l'octave, le rapport de 2 à 3 (rapport appelé hémiole - selon le grec - ou sesquialtère selon le terme latin) à la quinte, le rapport de 3 à 4 (épitrite ou sesquitierce) à la quarte, et le rapport de 9 à 8 (épogde ou sesquioctave) au ton. Ce passage difficile est interprété de manières différentes dans de nombreuses spéculations néoplatoniciennes, qui utilisent cette série pour décrire les rapports de distances entre les planètes — on peut évoquer notamment l'interprétation de Macrobe, dans le Commentaire au Songe de Scipion, II[/citation]
http://fr.wikipedia.org/wiki/Harmonie_des_sph%C3%A8res
[citation]" En premier lieu, il a séparé du mélange total une portion. Ensuite il a pris une seconde portion double de celle-là ; puis une troisième portion égale à une fois et demie la seconde et à trois fois la première ; une quatrième double de la seconde ; une cinquième triple de la troisième ; une sixième égale à huit fois la première ; une septième égale à vingt-sept fois la première. Après cela, il a comblé les intervalles doubles et triples, détachant encore des portions du mélange primitif et les disposant entre ces parties-là, de telle sorte que, dans chaque intervalle, il y eût deux médietés. La première surpasse les extrêmes ou est surpassée par eux d’une même fraction de chacun d’eux. La seconde surpasse les extrêmes d’une quantité égale à celle dont elle est elle-même surpassée. De ces relations naissent dans les intervalles ci-dessus désignés, des intervalles nouveaux de un plus un demi, un plus un tiers, un plus un huitième. A l’aide de l’intervalle de un plus un huitième, le Dieu a comblé tous les intervalles de un plus un tiers, laissant subsister de chacun d’eux une fraction telle que l’intervalle restant fût défini par le rapport du nombre deux cent cinquante-six au nombre deux cent quarante-trois. Et ainsi, le mélange dans lequel il avait coupé ces parties se trouva employé tout entier " (2)
Nous devons à Boeckh d'avoir résolu l'énigme de l'âme du monde au 19°siècle. Rivaud, parmi d'autres, en donne une interprétation complète, condensée ici en quelques schémas (consulter aussi les notes qui accompagnent une traduction récente de Luc Brisson).
La première division du mélange consiste en l'imbrication de deux suites géométriques, l'une de raison 2 (intervalles doubles) soit 1 : 2 : 4 : 8, l'autre de raison 3 (intervalles triples) 1 : 3 : 9 : 27.(3)[/citation]
http://ww3.ac-poitiers.fr/arts_p/b@lise13/pageshtm/page_5.htm
Je pense que Pythagore, Platon et autres ont mit de l'avant ces nombres bien avant que la valeur de la seconde soit unifiée en 1967. Je ne veux pas élaborer sur le Démiurge ici. Mais ce sont ces nombres que les Pythagoriens et Platon utilisent. Beacoup de lectures reprennent ces nombres bien avant 1967.
Pour le filtre, je suis bien daccord avec tout ce que tu dis en théorie... mais je suis sur de moi. J'ai vraiment passé bcp, bcp, bcp de temps sur l'élaboration de ce filtre et mes oreilles percoivent très bien la différence au final. J'utilise SpectraPlus et TuneLab Pro. Je ne suis pas au 0.0000000001 près quand même, j'en suis consient. Mais plutôt au 0.002 Hz près. Pas besoin d'analyseur de spectre pour comparer 2 dents de scie (pourquoi une dent de scie? pour les harmoniques) détuné de 0.002 Hz. On peut percevoir à l'oreille le battement (0.002 Hz) sur plusieurs secondes (moins d'une minute quand même!). Même un rapport de quinte en utilisant 1 dents de scie, on perçoit la différence de 0.002 Hz.
Si (j'ai bien dit si!) ça t'interesse xoC, je peux t'envoyer un patch du filtre que j'ai fais pour le Nord G2.
[citation]Un key follow bien programmé va suivre le pitch total : c'est à dire midi note + fine tune. D'ailleurs les effets midi qui permettent de décaler une gamme[/citation]
J'utilise l'entrée FM Lin/Trk avec des valeurs différentes pour l'OSC et pour le filtre. Car pour la même valeur MIDI (0), les valeurs en Hz ne sont pas les mêmes. 13.75 HZ pour le filtre et 8.0187 HZ pour l'OSC. Le calcul pour l'entrée FM ne se fait pas comme pour l'entrée de pitch. Je ne travaille pas sur un architecture fermé. En modulaire on contourne et on trouve des solutions comme on peu.
[citation]Pour ma part j'opterais pour 52 800 Hz
Je suis assez curieux d'entendre ton explication la dessus [/citation]
[/citation]
Pourquoi tu demandes si tu sais ? Effectivement après un overdose de fumette.. je me suis retrouvé en plein voyage astal. J'ai survollé l'Amérique, l'Europes, même le forum de Trance-Goa et j'ai eu cette révélation 52800
Merci pour les précisions sur les violons, c'est intéressant.
[citation]Et non, ne t'inquiète pas, cela ne me dérange jamais de débattre de son[/citation]
je pensais plus au fait de mentionner des détails privés. Oreille absolue, que tu possèdes un vivi, etc...
et alors ?[/citation]
et alors rien ! Je le mentionne car je n'ai pas vu personne en parler ailleur. Si ca peut aider ceux qui "jonglent" avec les nombres !
Voici comment on calcul :
LA/432 : 4+3+2 = 9 (facile!)
SI/486 : 4+8+6 = 18 , 1 + 8 = 9
SI/3888 : 3+8+8+8 = 27, 2 + 7 = 9
G#/410.0625 : 4+1+0+0+6+2+5 = 18, 1+ 8 = 9
A#/461.3203125 4+6+1+3+2+0+3+1+2+5 = 27, 2+7 = 9
etc...
[citation]Sauf que cette notion de nombre entier en parlant de fréquence n'avait aucun sens avant que la valeur de la seconde soit unifiée en 1967[/citation]
Pythagore utilise les rapports entiers et les proportions. Lorsqu'on pince un monocorde en son centre on obtient un rapport d'octave (1/2) et ainsi de suite. Ce n'est pas calculer en seconde. Si le temps est relatif, les rapports et les proportions ne le sont pas.
[citation]Platon, dans le Timée, décrit comment le Démiurge façonne l'Âme du monde. J.-Fr. Mattéi résume : "Le démiurge va tirer de sa composition finale une structure harmonique suggestive dont les calculs témoignent d'une influence pythagoricienne. Elle est constituée par une double progression géométrique de raison 2 (1, 2, 4, 8) et de raison 3 (1, 3, 9, 27), qu'il est commode de disposer sur un diagramme en forme de lambda majuscule (Λ
 , selon un schéma que l'on trouve chez Proclus. Cette figure porte, sur chaque côté de l'angle, les nombres respectifs de la série paire et de la série impaire. Le dernier de ces nombres (27) est égal à la somme des six précédents (1 + 2 + 3 + 4 + 8 + 9 = 27)... La progression selon le facteur 2 donne les octaves par doublement successifs des intervalles (1, 2, 4, 8 = Do1, Do2, Do3, Do4...), alors que la progression selon le facteur 3 forme les douzièmes justes (1 = Do, 3 = Sol, 9 = Ré, 27 = La, 81 = Mi, 243 = SI...). On peut alors combler les intervalles musicaux doubles ou triples pour former la gamme complète en s'aidant de deux proportions continues ou 'médiétés', l'une arithmétique (de type 1, 2, 3), l'autre harmonique (de type 3, 4, 6), bien connues des pythagoriciens, en particulier Archytas. L'intervalle des nombres de 1 à 2 sera composé des nombres 1 (Tonique), 4/3 (Quarte), 3/2 (Quinte) et 2 (Octave) ; le ton, dont la valeur est 9/8, se situe entre la quarte et la quinte, puisque 3/2 : 4/3 = 9/8. L'Âme du monde est ainsi composée de cinq tons majeurs égaux entre lesquels est intercalé comme 'reste', leimma, l'intervalle de 256/243 (= 1,053), mesure du demi-ton diatonique de la gamme naturelle de Pythagore, qui est un peu plus faible que notre demi-ton tempéré (16/15 = 1,066)"[/citation]
, selon un schéma que l'on trouve chez Proclus. Cette figure porte, sur chaque côté de l'angle, les nombres respectifs de la série paire et de la série impaire. Le dernier de ces nombres (27) est égal à la somme des six précédents (1 + 2 + 3 + 4 + 8 + 9 = 27)... La progression selon le facteur 2 donne les octaves par doublement successifs des intervalles (1, 2, 4, 8 = Do1, Do2, Do3, Do4...), alors que la progression selon le facteur 3 forme les douzièmes justes (1 = Do, 3 = Sol, 9 = Ré, 27 = La, 81 = Mi, 243 = SI...). On peut alors combler les intervalles musicaux doubles ou triples pour former la gamme complète en s'aidant de deux proportions continues ou 'médiétés', l'une arithmétique (de type 1, 2, 3), l'autre harmonique (de type 3, 4, 6), bien connues des pythagoriciens, en particulier Archytas. L'intervalle des nombres de 1 à 2 sera composé des nombres 1 (Tonique), 4/3 (Quarte), 3/2 (Quinte) et 2 (Octave) ; le ton, dont la valeur est 9/8, se situe entre la quarte et la quinte, puisque 3/2 : 4/3 = 9/8. L'Âme du monde est ainsi composée de cinq tons majeurs égaux entre lesquels est intercalé comme 'reste', leimma, l'intervalle de 256/243 (= 1,053), mesure du demi-ton diatonique de la gamme naturelle de Pythagore, qui est un peu plus faible que notre demi-ton tempéré (16/15 = 1,066)"[/citation]http://fr.wikipedia.org/wiki/Symbolisme_des_nombres
[citation]dans lequel Platon décrit la fabrication des proportions de l'Âme du Monde par le Démiurge. Ce passage est fondé sur la série numérique 1, 2, 3, 4, 9, 8, 27 — qui correspond à la fusion de la série des premières puissances de 2 (2, 4, 8) et de la série des premières puissances de 3 (3, 9, 27). Or, de cette série, on peut tirer les rapports numériques sur lesquels sont fondés les intervalles musicaux : le rapport de 1 à 2 (rapport double) correspond à l'octave, le rapport de 2 à 3 (rapport appelé hémiole - selon le grec - ou sesquialtère selon le terme latin) à la quinte, le rapport de 3 à 4 (épitrite ou sesquitierce) à la quarte, et le rapport de 9 à 8 (épogde ou sesquioctave) au ton. Ce passage difficile est interprété de manières différentes dans de nombreuses spéculations néoplatoniciennes, qui utilisent cette série pour décrire les rapports de distances entre les planètes — on peut évoquer notamment l'interprétation de Macrobe, dans le Commentaire au Songe de Scipion, II[/citation]
http://fr.wikipedia.org/wiki/Harmonie_des_sph%C3%A8res
[citation]" En premier lieu, il a séparé du mélange total une portion. Ensuite il a pris une seconde portion double de celle-là ; puis une troisième portion égale à une fois et demie la seconde et à trois fois la première ; une quatrième double de la seconde ; une cinquième triple de la troisième ; une sixième égale à huit fois la première ; une septième égale à vingt-sept fois la première. Après cela, il a comblé les intervalles doubles et triples, détachant encore des portions du mélange primitif et les disposant entre ces parties-là, de telle sorte que, dans chaque intervalle, il y eût deux médietés. La première surpasse les extrêmes ou est surpassée par eux d’une même fraction de chacun d’eux. La seconde surpasse les extrêmes d’une quantité égale à celle dont elle est elle-même surpassée. De ces relations naissent dans les intervalles ci-dessus désignés, des intervalles nouveaux de un plus un demi, un plus un tiers, un plus un huitième. A l’aide de l’intervalle de un plus un huitième, le Dieu a comblé tous les intervalles de un plus un tiers, laissant subsister de chacun d’eux une fraction telle que l’intervalle restant fût défini par le rapport du nombre deux cent cinquante-six au nombre deux cent quarante-trois. Et ainsi, le mélange dans lequel il avait coupé ces parties se trouva employé tout entier " (2)
Nous devons à Boeckh d'avoir résolu l'énigme de l'âme du monde au 19°siècle. Rivaud, parmi d'autres, en donne une interprétation complète, condensée ici en quelques schémas (consulter aussi les notes qui accompagnent une traduction récente de Luc Brisson).
La première division du mélange consiste en l'imbrication de deux suites géométriques, l'une de raison 2 (intervalles doubles) soit 1 : 2 : 4 : 8, l'autre de raison 3 (intervalles triples) 1 : 3 : 9 : 27.(3)[/citation]
http://ww3.ac-poitiers.fr/arts_p/b@lise13/pageshtm/page_5.htm
Je pense que Pythagore, Platon et autres ont mit de l'avant ces nombres bien avant que la valeur de la seconde soit unifiée en 1967. Je ne veux pas élaborer sur le Démiurge ici. Mais ce sont ces nombres que les Pythagoriens et Platon utilisent. Beacoup de lectures reprennent ces nombres bien avant 1967.
Pour le filtre, je suis bien daccord avec tout ce que tu dis en théorie... mais je suis sur de moi. J'ai vraiment passé bcp, bcp, bcp de temps sur l'élaboration de ce filtre et mes oreilles percoivent très bien la différence au final. J'utilise SpectraPlus et TuneLab Pro. Je ne suis pas au 0.0000000001 près quand même, j'en suis consient. Mais plutôt au 0.002 Hz près. Pas besoin d'analyseur de spectre pour comparer 2 dents de scie (pourquoi une dent de scie? pour les harmoniques) détuné de 0.002 Hz. On peut percevoir à l'oreille le battement (0.002 Hz) sur plusieurs secondes (moins d'une minute quand même!). Même un rapport de quinte en utilisant 1 dents de scie, on perçoit la différence de 0.002 Hz.
Si (j'ai bien dit si!) ça t'interesse xoC, je peux t'envoyer un patch du filtre que j'ai fais pour le Nord G2.

[citation]Un key follow bien programmé va suivre le pitch total : c'est à dire midi note + fine tune. D'ailleurs les effets midi qui permettent de décaler une gamme[/citation]
J'utilise l'entrée FM Lin/Trk avec des valeurs différentes pour l'OSC et pour le filtre. Car pour la même valeur MIDI (0), les valeurs en Hz ne sont pas les mêmes. 13.75 HZ pour le filtre et 8.0187 HZ pour l'OSC. Le calcul pour l'entrée FM ne se fait pas comme pour l'entrée de pitch. Je ne travaille pas sur un architecture fermé. En modulaire on contourne et on trouve des solutions comme on peu.
[citation]Pour ma part j'opterais pour 52 800 Hz
Je suis assez curieux d'entendre ton explication la dessus
 [/citation]
[/citation]Pourquoi tu demandes si tu sais ? Effectivement après un overdose de fumette.. je me suis retrouvé en plein voyage astal. J'ai survollé l'Amérique, l'Europes, même le forum de Trance-Goa et j'ai eu cette révélation 52800
Merci pour les précisions sur les violons, c'est intéressant.
[citation]Et non, ne t'inquiète pas, cela ne me dérange jamais de débattre de son[/citation]
je pensais plus au fait de mentionner des détails privés. Oreille absolue, que tu possèdes un vivi, etc...
bon ben jve demander a xoc alors vu que t'as l'air assez doué dans les phases aussi kbbk ^^ pourquoi 52800 Hz
Quand je te parle de la valeur de la seconde non unifiée avant 1967, c'est surtout pour dire à quel point une mesure de 432 Hz précise, avec d'autres notes qui ont des fréquences entières, n'a aucun sens. Je ne critique pas les histoires de rapports de fréquences de la gamme de Pythagore, qui eux ont bien entendu un sens.
D'ailleurs je viens de passer à Cubase 7.5, et le hermode tuning est maintenant intégré directement dedans, c'est cool ça
Bien sûr qu'on peut entendre 0.002 Hz de décalage si deux sons jouent en même temps, je n'ai jamais dit le contraire la dessus. Mais pour le filtre, désolé mais c'est loin d'être un concept qui a besoin d'une précision absolue sur la valeur de fréquence pour fonctionner. La bande de transition est très large, cf les deux photos suivantes : gain/phase et gain/groupe delay :
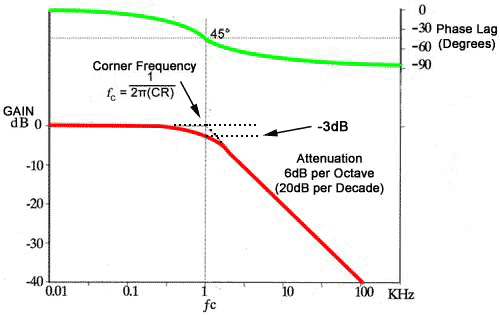

Quant aux fréquences d'échantillonnage, je vous donne un peu de lecture sérieuse :
http://www.lavryengineering.com/lavry-white-papers/
[citation]je pensais plus au fait de mentionner des détails privés. Oreille absolue, que tu possèdes un vivi, etc... [/citation]
C'est gentil de demander, mais vu que j'en ai déjà parlé ici même, c'est que ce n'est pas tabou
D'ailleurs je viens de passer à Cubase 7.5, et le hermode tuning est maintenant intégré directement dedans, c'est cool ça

Bien sûr qu'on peut entendre 0.002 Hz de décalage si deux sons jouent en même temps, je n'ai jamais dit le contraire la dessus. Mais pour le filtre, désolé mais c'est loin d'être un concept qui a besoin d'une précision absolue sur la valeur de fréquence pour fonctionner. La bande de transition est très large, cf les deux photos suivantes : gain/phase et gain/groupe delay :


Quant aux fréquences d'échantillonnage, je vous donne un peu de lecture sérieuse :
http://www.lavryengineering.com/lavry-white-papers/
[citation]je pensais plus au fait de mentionner des détails privés. Oreille absolue, que tu possèdes un vivi, etc... [/citation]
C'est gentil de demander, mais vu que j'en ai déjà parlé ici même, c'est que ce n'est pas tabou

merci pr le link xoc nikwell